\[ \newcommand{\bs}[1]{\boldsymbol{#1}} \newcommand{\dfrac}[2]{\displaystyle\frac{\text{d}{#1}}{\text{d}{#2}}} \newcommand{\ddfrac}[2]{\displaystyle\frac{\text{d}^2{#1}}{\text{d}{#2}^2}} \]
本章では, 有限要素法 (finite element method; FEM) の概念を説明することを目的とし, \(x\in[0,1]\) で定義された二階常微分方程式
\[ \frac{\text{d}^2 u(x)}{\text{d} x^2} = -f(x) \qquad(1)\]
を対象とした有限要素法について述べる. ここに, \(u(x)\) は未知のスカラー関数, \(f(x)\) は既知のスカラー関数である.
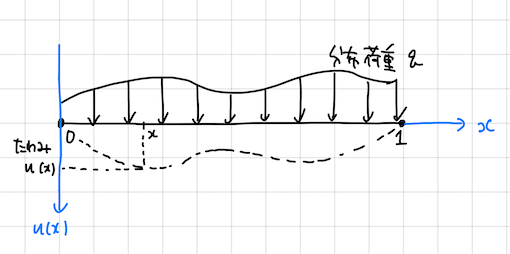
はじめに, 弦のたわみが式 ( 1) で記述される物理現象 (の一つ) であることを確認しよう. 今, 図 1 のように, 両端が固定された長さ 1 の弦に, 下向き分布荷重 \(q(x)\) が作用した時, 点 \(x\) におけるたわみ \(v(x)\) を求める問題を考えよう. なお, 荷重は下向きに作用するので, 縦軸は下向きを正にとる.

微小領域 \([x,x+\text{d}x]\) における弦に作用する力の釣り合いを考える (図 2).
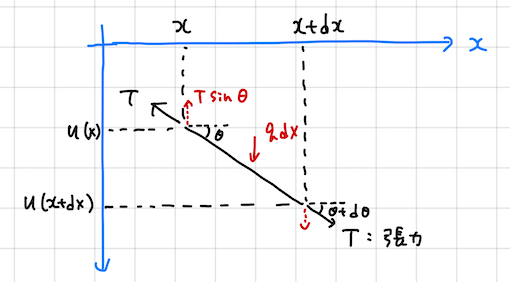
弦に働く張力を \(T\) と書き, 変形が微小であることを仮定すれば \(\sin\theta\simeq\tan\theta=\displaystyle\frac{\text{d}u(x)}{\text{d}x}\) だから, 左端 \(x\) に作用する張力の鉛直方向成分は \(-T\sin\theta\simeq-T\dfrac{u(x)}{x}\) と書ける. 同様にして, 右端 \(x+\text{d}x\) に作用する張力の鉛直方向成分は
\[ T\dfrac{u(x+\text{d}x)}{x} \simeq T\left(\dfrac{u(x)}{x}+\ddfrac{u(x)}{x}\text{d}x\right) \]
である. さらに, 与えられた分布荷重が微小領域において一定値 \(q(x)\) を取るとすれば, 力の釣り合いは
\[ -T\dfrac{u(x)}{x}+T\left(\dfrac{u(x)}{x}+\ddfrac{u(x)}{x}\text{d}x\right)+q(x)\text{d}x=0 \]
と書ける. これを整理して, \(f(x)=q(x)/T\) とおけば式 ( 1) を得る.
今, 弦は両端で固定されているので, 境界条件は
\[ u(0)=u(1)=0 \qquad(2)\]
である. 微分方程式 ( 1) と境界条件 ( 2) の組みを境界値問題 (boudnary value problem; BVP) と呼ぶ. 有限要素法は境界値問題の数値解法のひとつである. なお, 式 ( 2) のように, 未知関数そのものの境界値を与える境界条件を Dirichlet 境界条件という. 一方で, 未知関数の境界での微分値を与える境界条件は Neumann 境界条件, Dirichlet 条件と Neumann 条件の線形結合を与える境界条件は Robin 境界条件と呼ばれる.
問: \(f(x)=1\) のとき, 上の Dirichlet 境界値問題の解を解析的に (=手計算で積分し) 求めよ. 特に, \(x=1/2\) における \(u\) の値はいくらか?
解: \(u(x)=-\displaystyle\frac{1}{2}x^2+\displaystyle\frac{1}{2}x\) であり, 特に \(u(1/2)=1/8\) となる.
先の「問」においては, 微分方程式を解析的に解くことができた. しかし, 一般にはこれは難しい. そこで \(u\) をなんらかの意味で近似する関数 \(\tilde{u}\) を求めることが必要となる. 以下, \(\tilde{u}\) を求める方法の一つである重み付き残差法について解説する.
まず, \(\tilde{u}\) が \(u\) が満たすべき境界条件 ( 2) を満足することを要請しよう. すると, \(g_i(0)=g_i(1)=0\) を満たす関数 \(g_i(x)\) (例えば \(g_i(x)=x^{i+1}(1-x)\) など, \(g_i\) は基底関数と呼ばれる) を用いて構成される
\[ \sum_{i=0}^{n-1} a_i g_i(x) \qquad(3)\]
は \(\tilde{u}\) の候補となる. ここに, \(a_i\in\mathbb{R}\) は未知の係数である. 未知係数 \(a_i\) を求めるため, ここでは重み付き残差法を採用する. その他の方法としては, 微分方程式の定義された領域内部の有限個の点 \(x_i \ (i=0,\cdots, n-1)\) において微分方程式を満たすように \(a_i\) を決める選点法が代表的である.
はじめに, 適当な重み関数 \(v_i(x)\) を \(i=0, \cdots, n-1\) の \(n\) 種類準備する. 次に, 微分方程式 ( 1) の両辺にこれを乗じ, 微分方程式の定義された領域 \([0, 1]\) において積分すると以下を得る.
\[ \int_0^1 v_i \left( \ddfrac{\tilde{u}(x)}{x}+f(x) \right) \text{d}x=0 \qquad(4)\]
式 ( 4) を重み付き残差式と呼ぶ. これを満たすように未知係数 \(a_i\) を定める方法を重み付き残差法である.
例: \(f(x)=1\)の場合を考える. \(n=1\), \(g_i(x)=\sin (i+1) \pi x\) とし, 重み付き残差法を実行せよ. ただし, ここでは重み関数は以下のように選べ.
- \(v_i(x)=1\)
- \(v_i(x)=g_i(x)\) (このように, 解を展開するのに用いた基底 \(g_i\) と同じ関数を重みとする方法を Galerkin 法 という)
解
重み付き残差式 ( 4) より,
\[ \begin{align} 0 &=\int_0^1 \left( \ddfrac{(a_0 \sin\pi x)}{x}+1 \right) \text{d}x\\ &=\int_0^1 \left( -a_0\pi^2\sin\pi x+1 \right) \text{d}x\\ &=\left[ a_0\pi\cos\pi x +x \right]_0^1\\ &=-2a_0\pi+1 \end{align} \]
であるから, \(a_0=1/2\pi\) を得る. この時, \(u\) の近似解は \(\tilde{u}(x)=\displaystyle\frac{1}{2\pi}\sin\pi x\) となる. 特に, \(\tilde{u}(1/2)=1/2\pi\) であるが, ここで得た近似解と先に求めた「正解」との相対誤差は \[ \frac{|1/2\pi-1/8|}{1/8} \simeq 27.3\% \]
ほどである.
重み付き残差式 ( 4) より,
\[ \begin{align} 0 &=\int_0^1 \sin\pi x\left( \ddfrac{(a_0 \sin\pi x)}{x}+1 \right) \text{d}x\\ &=\int_0^1 \sin\pi x \left( -a_0\pi^2\sin\pi x+1 \right) \text{d}x\\ &=\left[ -\frac{a_0\pi}{2}x-\frac{1}{\pi}\cos\pi x \right]_0^1\\ &=-\frac{a_0\pi^2}{2}+\frac{2}{\pi} \end{align} \]
であるから, \(a_0=4/\pi^3\) を得る. この時, \(u\) の近似解は \(\tilde{u}(x)=\displaystyle\frac{4}{\pi^3}\sin\pi x\) となる. 特に, \(\tilde{u}(1/2)=4/\pi^3\) であるが, ここで得た近似解と先に求めた「正解」との相対誤差は \[ \frac{|4/\pi^3-1/8|}{1/8} \simeq 3.20\%\] ほどである.
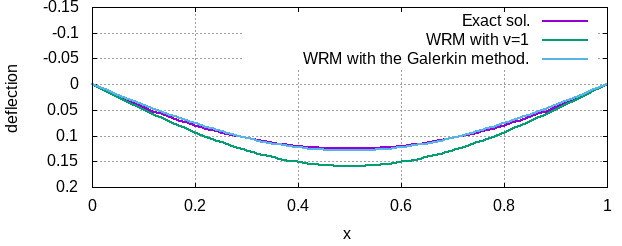
例題の 1, 2 で得られた「数値解」と「正解」の様子を 図 3 に示す. Galerkin 法が高精度であることが先に示した誤差, 図からよく分かるであろう. なお, Galerkin 法や選点法を用いることで, 関数を求める問題であった境界問題が, 有限個の係数 \(a_i\) (\(n=0,\cdots, n-1\)) を求める問題に変わったことに注意されたい. この意味で, Galerkin 法や選点法を 離散化 手法と呼ぶことがある.
先の問題に対し, \(\tilde{u}=a_0 x(1-x) + a_1 x^2(1-x)\) とした時, 重み付き残差式 ( 4) を Galerkin 法で離散化し, 未知係数 \(a_i\) を求めよ.
さて, 前項では, 重み付き残差式 ( 4) をそのまま利用した. ここでは, これを少し変形してみよう. ここでは, 重み関数 \(v_i\) として, Dirichlet 境界条件が課された境界において, \(v_i=0\) を満たすものを用いると約束しよう. この時, 重み付き残差式 ( 4) を部分積分して得られる
\[ \begin{align} &0=\left[ u'(x)v_i(x) \right]_0^1 - \int_0^1 (v_i'(x)u'(x)-v_i(x)f(x)) \text{d}x\\ &\Leftrightarrow \int_0^1 v_i'(x)u'(x) \text{d}x = \int_0^1 v_i(x)f(x) \text{d}x \ \ \ (\because v_i(0)=v_i(1)=0) \end{align} \qquad(5)\]
を弱形式 (weak form) という. これに対応して, もとの微分方程式 ( 1) を強形式と呼ぶことがある. ここで, 強形式には \(u\) の二階微分が含まれている一方で, 弱形式には \(u\) の一階微分しか現れないことに注意されたい. したがって, 弱形式化することにより, \(u\) の近似解 \(\tilde{u}\) の基底として, 図 4 に示すような区分的に一次の関数を用いることができる (\(\tilde{u}(x)=a_0g_0(x)+a_1g_1(x)\) の二階微分は恒等的に零であることに注意).
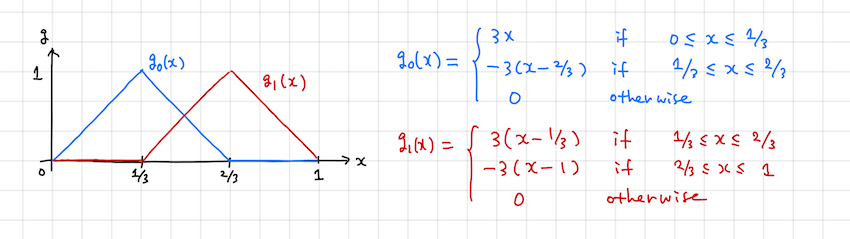
弱形式 ( 5) を Galerkin 法で離散化して未知係数 \(a_i\) を求める手順は, 先に見た (弱形式を用いない) 重み付き残差法の場合と同様であり, 基底で展開した \(\tilde{u}(x)=\displaystyle\sum_{i=0}^{n-1} a_i g_i(x)\) を弱形式 5 に代入して得られる代数方程式 (=ここでは連立一次方程式となる)
\[ \sum_{j=0}^{n-1} \left( \int_0^1 g_i'(x) g_j'(x) \mathrm{d}x\right) a_{j} = \int_0^1 g_i f(x) \mathrm{d}x \qquad(6)\]
\((i=0,\cdots,n-1)\) を解けば良い.
例: \(f(x)=1\)の場合を考える. 図 4 に示す基底関数を用い, 弱形式 ( 5) に基づき未知係数 \(a_i\) を求めよ.
この時, 代数方程式 ( 6) は
\[ \begin{pmatrix} \int_0^1 g_0'(x)g_0'(x) \mathrm{d}x& \int_0^1 g_0'(x)g_1'(x) \mathrm{d}x \\ \int_0^1 g_1'(x)g_0'(x) \mathrm{d}x& \int_0^1 g_1'(x)g_1'(x) \mathrm{d}x \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \end{pmatrix} = \begin{pmatrix} \int_0^1 g_0(x) \mathrm{d}x\\ \int_0^1 g_1(x) \mathrm{d}x \end{pmatrix} \]
となる. 積分を実行し, 代数方程式を解けば, \(a_0=a_1=1/9\) を得る. この時, 近似解は 図 5 のようである.
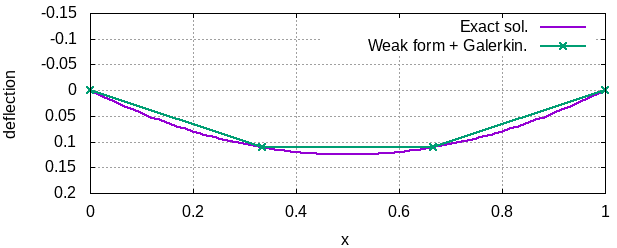
先の例において, 基底関数として以下
\[ \begin{align} g_0(x)&=\begin{cases} 4x & \text{if } 0\le x\le 1/4 \\ -4(x-1/2) & \text{if } 0\le x\le 1/2 \\ 0 & \text{otherwise} \end{cases}\\ g_1(x)&=\begin{cases} 4(x-1/4) & \text{if } 1/4\le x\le 1/2 \\ -4(x-3/4) & \text{if } 1/2\le x\le 3/4 \\ 0 & \text{otherwise} \end{cases}\\ g_2(x)&=\begin{cases} 4(x-1/2) & \text{if } 1/2\le x\le 3/4 \\ -4(x-1) & \text{if } 3/4\le x\le 1 \\ 0 & \text{otherwise} \end{cases} \end{align} \]
を用い, 弱形式を Galerkin 法で離散化することにより近似解 \(\tilde{u}\) を求め, その誤差について論ぜよ.
ここで紹介した基底関数は, 先に用いた \(x(x-1)\) などとは異なり, その台が微分方程式 ( 1) の定義域全体にわたらない. すなわち, 区間 \(\mathrm{supp.}(g_i):=\{x \mid g_i(x)>0\}\) が \([0,1]\) に一致しない. このような性質を局所的な台を持つ (locally supported) と言う. 基底関数が局所的な台を持つとき, 有限要素法に由来する代数方程式 ( 6) の係数行列は疎行列 (sparse matrix) となる. すなわち, 行列の成分のほとんどが零となる. 通常, 代数方程式 ( 6) の求解においては, 係数行列が疎であることを利用した高速なアルゴリズムを用いる.
以上をまとめると, 有限要素法とは, 微分方程式 (一般には偏微分方程式) の境界値問題の近似解を求める方法であり, 局所的な台を持つ基底関数で解を展開し, 重み付き残差式に対応する弱形式を, Galerkin 法で離散化して得られる代数方程式を計算機を用いて解く方法である.
次の微分方程式の境界値問題
\[ \begin{align} \frac{\text{d}^2 u(x)}{\text{d} x^2} = -f(x) \qquad x\in[0,1] \\ f(x)=\begin{cases} 1 & \mathrm{if~} x\le 1/2\\ 0 & \mathrm{otherwise} \end{cases}\\ u(0)=u(1)=0 \end{align} \]
に対し, 適当な基底関数を用いて有限要素法を実行し, \(u\) の近似解を求めよ.